Mirror Hands (4)

—  MORE ABOUT SYMMETRY  —

Suppose, for example, that each hand is arranged in some 5-4-3-1 pattern.  This means that each suit also is divided 5-4-3-1 around the table.

For each deal there are six different configurations of the four hands.  Example: from a south perspective, each of the other three hands could be north, and in each case either of the two remaining hands could be east.  3 partners × 2 RHO's = 6.  However, an exchange of, say, the east and south hands, would result in a non-symmetrical arrangement; so some suit-swapping is necessary in order to achieve a mirror-type position.

A simple exchange of the east-west hands often makes no difference in the total tricks.  For example, such a swap in the 5-5-2-1 example on Page 2 would not enable any player to make a contract.  Occasionally, however, the difference can be dramatic.  Consider the magic 3NT contract on the previous page.  By exchanging the east and west hands, the tables are completely turned, because whichever side is on lead can win nine tricks!

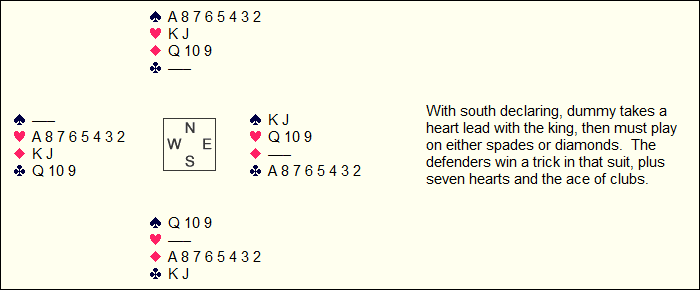
Let us rearrange some suits around the north hand.  Now each side has a pair of 8-2 fits instead of 8-3.

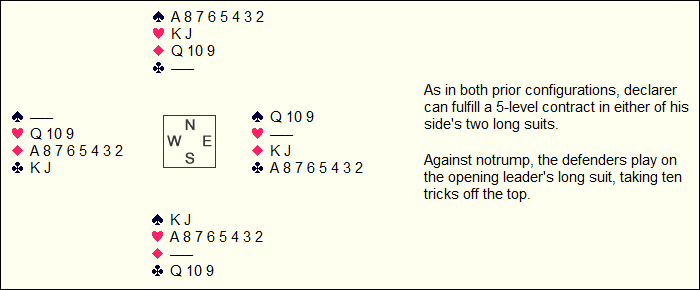
Swapping the east and west hands:

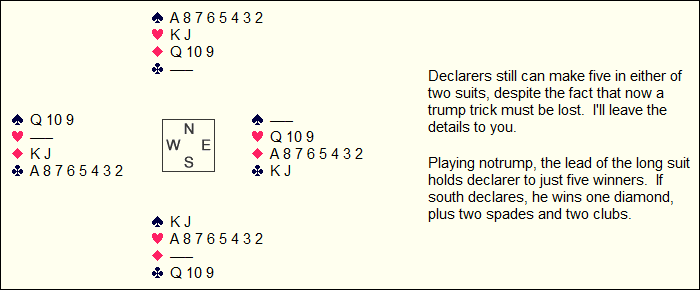
Finally, the suit fits are set to 8-0:

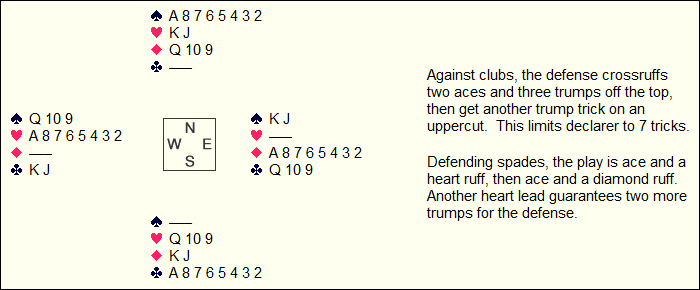
With the east and west hands swapped, the results are the same.

Note: when the hands have two voids, there are only two meaningful variations — whether the two sides have a fit or not.  Example: in a 7-6-0-0 mirror hand with no fits, if south leads one his seven spades, it makes no difference which opponent has the other six cards in that suit!  In fact, the sequence of plays would remain unchanged even if the rotation of play were to be reversed to counter-clockwise.

Conclusion: this investigation has been most enlightening, albeit immensely time-consuming.  I hope you agree that somebody had to do it.